机器学习是现代人工智能的核心，支撑着从推荐系统到自动驾驶汽车等各类应用。但每一个智能应用背后，都离不开那些奠定基础的模型。本文将为你简明而全面地梳理关键的机器学习模型，帮助你系统掌握核心概念与应用。
线性回归（Linear Regression）
线性回归旨在通过寻找一条“最佳拟合直线”，来建立自变量与因变量之间的关系。它使用最小二乘法（least square method），使所有数据点到直线的距离之和最小化。最小二乘法通过最小化残差平方和（SSR，Sum of Squared Residuals），来确定最终的线性方程。
例如，下图中的绿色直线相比蓝色直线拟合得更好，因为它与所有数据点的距离更小。
图片
Lasso 回归（L1 正则化）
Lasso 回归是一种正则化技术，通过在模型中引入一定的偏差来减少过拟合。它的做法是在最小化残差平方差的基础上，增加一个惩罚项，这个惩罚项等于 λ（lambda）乘以斜率的绝对值。这里的 λ 表示惩罚的强度，是一个可以调整的超参数，用来控制过拟合并获得更好的拟合效果。
Lasso 回归的代价函数
当特征数量较多时，L1 正则化通常是更优的选择，因为它可以忽略掉那些斜率值非常小的变量，从而实现特征选择。
展示正则化对过拟合回归线影响的图表
Ridge 回归（L2 正则化）
Ridge 回归与 Lasso 回归非常相似，唯一的区别在于惩罚项的计算方式。它在损失函数中增加了一个惩罚项，这个惩罚项等于各系数幅值的平方乘以 λ（lambda）。
Ridge 回归的代价函数
当数据中存在多重共线性（即自变量之间高度相关）时，L2 正则化是更好的选择，因为它可以将所有系数收缩（Shrinkage）向零，从而缓解共线性问题。
Elastic Net 回归
Elastic Net 回归结合了 Lasso 回归和 Ridge 回归的惩罚项，从而得到一个更加正则化的模型。它可以在两种惩罚之间取得平衡，通常比单独使用 L1 或 L2 正则化获得更优的模型性能。
图片
多项式回归（Polynomial Regression）
多项式回归将因变量与自变量之间的关系建模为一个 n 次多项式。多项式是由形如 k·xⁿ 的各项之和组成的，其中 n 是非负整数，k 是常数，x 是自变量。多项式回归主要用于处理非线性数据。
在非线性数据上拟合简单线性回归线与多项式回归线的对比
逻辑回归（Logistic Regression）
逻辑回归是一种分类技术，旨在为数据找到最佳拟合曲线。它使用Sigmoid 函数将输出值压缩到 0 到 1 的范围内。不同于线性回归通过最小二乘法寻找最佳拟合直线，逻辑回归采用最大似然估计（MLE）来确定最佳拟合曲线。
线性回归与逻辑回归在二分类输出上的对比
K 近邻算法（K-Nearest Neighbours，KNN）
KNN 是一种分类算法，它根据新数据点与已分类数据点之间的距离进行分类。它假设彼此接近的数据点具有高度相似性。
由于 KNN 在训练阶段仅存储数据而不进行实际分类，直到遇到新的数据点进行预测，因此被称为懒惰学习算法（lazy learner）。
默认情况下，KNN 使用欧几里得距离来寻找新数据点最近的已分类数据点，并通过最近邻居中出现次数最多的类别（众数）来确定新数据点的预测类别。
如果 k 值设置得过小，新数据点可能被误判为异常值；如果 k 值设置得过大，则可能忽略样本数量较少的类别。
应用 KNN 前后的数据分布变化
朴素贝叶斯（Naive Bayes）
朴素贝叶斯是一种基于贝叶斯定理的分类技术，主要用于文本分类。
贝叶斯定理描述了在已知与事件相关的条件的先验知识基础上，计算事件发生的概率。它的公式如下所示：
贝叶斯定理公式
朴素贝叶斯被称为“朴素”的原因是，它假设某一特征的出现与其他特征的出现是相互独立的。
支持向量机（Support Vector Machines，SVM）
支持向量机的目标是找到一个超平面，在 n 维空间（即特征的数量为 n）中将数据点分割成不同的类别。这个超平面是通过最大化类之间的边距（即距离）来确定的。
支持向量是离超平面最近的数据点，它们能够影响超平面的定位和方向，帮助最大化类之间的边距。超平面的维度取决于输入特征的数量。
支持向量机在线性可分数据上的应用
决策树（Decision Tree）
决策树是一种基于树形结构的分类器，包含一系列条件语句，这些条件语句决定了样本沿着哪条路径走，直到到达树的底部。
决策树示例
决策树的内部节点表示特征，分支表示决策规则，叶节点表示结果。树的决策节点类似于 if-else 条件，叶节点包含决策节点的输出。
决策树的构建从选择一个特征作为根节点开始，使用特征选择度量（如 ID3 或 CART），然后递归地将剩余的特征与父节点进行比较，创建子节点，直到树达到其叶节点。
随机森林（Random Forest）
随机森林是一种集成技术，由多个决策树组成。在构建每个独立的决策树时，随机森林使用了自助法（bagging）和特征随机化，目的是创建一个无关的决策树森林。
随机森林中的每棵树都是在数据的不同子集上训练的，用于预测结果，然后选择大多数树投票的结果作为最终的预测值。
包含 4 个估计器的随机森林分类器
例如，如果我们只创建了一棵决策树，第二棵树的预测结果为类 0，但依赖于四棵树的众数后，我们的预测结果变成了类 1，这就是随机森林的强大之处。
极限随机树（Extra Trees）
极限随机树与随机森林分类器非常相似，唯一的区别在于它们选择根节点的方式。在随机森林中，使用最优特征进行分割，而在极限随机树分类器中，随机选择特征进行分割。极限随机树提供了更多的随机性，并且特征之间的相关性非常小。
另外，两者的另一个区别是，随机森林使用自助法（bootstrap replicas）生成大小为 N 的子集来训练集成成员（决策树），而极限随机树则使用整个原始样本。
由于极限随机树在训练到预测的整个过程中，每棵决策树的操作都是相同的，并且随机选择分割点，因此它的计算速度比随机森林快得多。
随机森林与极限随机树的比较
ADA Boost
ADA Boost 是一种提升算法，它与随机森林相似，但也有一些显著的区别：
- 与构建决策树森林不同，ADA Boost 构建的是决策树桩的森林。（决策树桩是只有一个节点和两个叶子的决策树）
- 每个决策树桩在最终决策中被赋予不同的权重。
- 它会对被错误分类的数据点赋予更高的权重，以便在构建下一个模型时，这些数据点能得到更多的关注。
- 它有助于将多个“弱分类器”组合成一个强分类器。
提升集成学习算法的一般过程
梯度提升（Gradient Boosting）
梯度提升通过构建多个决策树，其中每棵树都从前一棵树的错误中学习。它使用残差误差来提高预测性能。梯度提升的整个目标是尽可能减少残差误差。
梯度提升与 ADA Boost 相似，两者的区别在于，ADA Boost 构建决策树桩，而梯度提升则构建具有多个叶子的决策树。
梯度提升的过程从构建一棵基本的决策树开始，并做出初步预测，通常使用平均值作为初始预测。然后，通过使用初始特征和残差误差作为自变量，创建新的一棵决策树。对于新决策树的预测，是通过将模型的初始预测加上样本的残差误差乘以学习率得到的，整个过程会不断重复，直到我们达到最小误差为止。
K-Means 聚类
KMeans 聚类是一种无监督的机器学习算法，它将没有标签的数据分成 K 个不同的簇，其中 K 是用户定义的整数。
它是一个迭代算法，通过使用簇的质心（centroid）将没有标签的数据划分为 K 个簇，使得具有相似属性的数据点属于同一簇。
- 定义 K 并创建 K 个簇
- 计算每个数据点与 K 个质心的欧几里得距离
- 将最近的数据点分配给质心，并创建一个簇
- 通过计算均值重新计算质心
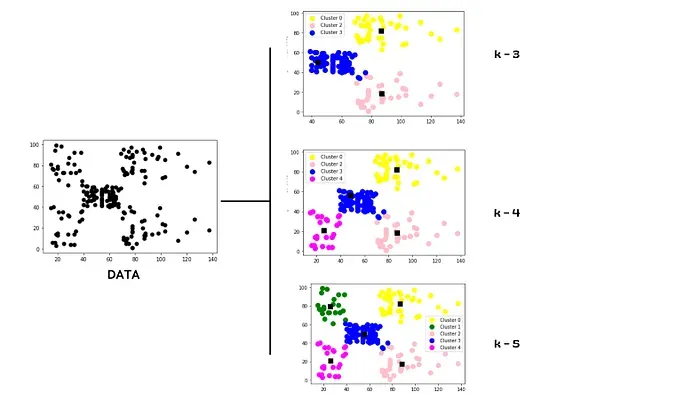使用不同 K 值的 K-Means 聚类对无标签数据进行聚类
层次聚类（Hierarchical Clustering）
层次聚类是另一种基于聚类的算法，它以树状结构的形式创建簇的层次，以划分数据。它自动发现数据之间的关系，并将它们划分为 n 个不同的簇，其中 n 是数据的大小。
层次聚类有两种主要方法：凝聚式（Agglomerative）和分裂式（Divisive）。
凝聚式和分裂式层次聚类在簇创建过程中的比较
在凝聚式聚类中，我们将每个数据点视为一个单独的簇，然后将这些簇合并，直到只剩下一个簇（即完整的数据集）。而分裂式层次聚类则从整个数据集（视为一个单独的簇）开始，然后将其划分为不太相似的簇，直到每个数据点成为一个独立的簇。
DBSCAN 聚类
DBSCAN（基于密度的空间聚类算法，带噪声）假设，如果一个数据点离一个簇的许多数据点比较近，而不是离某个单独的点很近，那么该数据点属于该簇。
图片
（图：来自 Wikipedia 的 DBSCAN 聚类示例，minPts = 4。点 A 和其他红点是核心点，因为这些点周围的 ε 半径内包含至少 4 个点（包括点 A 本身）。由于它们之间都可以相互到达，因此形成一个簇。点 B 和点 C 不是核心点，但可以通过其他核心点从 A 到达，因此它们也属于这个簇。点 N 是噪声点，既不是核心点，也不能直接从其他点到达。）
epsilon 和 min_points 是两个重要的参数，用于将数据划分为小簇。epsilon 指定了一个点需要与另一个点多近才能认为它是簇的一部分，而 min_points 则决定了形成一个簇所需的最小数据点数。
Apriori 算法
Apriori 算法是一种关联规则挖掘算法，它通过分析数据项之间的依赖关系，将相关的数据项关联在一起。
使用 Apriori 算法创建关联规则的关键步骤包括：
- 确定每个大小为 1 的项集的支持度，其中支持度是数据集中项出现的频率。
- 剪枝所有低于最小支持度阈值的项（由用户决定）。
- 创建大小为 n+1 的项集（n 是前一个项集的大小），并重复步骤 1 和 2，直到所有项集的支持度都超过阈值。
- 使用置信度生成规则（即在已知 x 出现的情况下，x 和 y 一起出现的频率）。
分层 K 折交叉验证 (Stratified K-fold Cross-Validation)
分层 K 折交叉验证是 K 折交叉验证的一个变体，它使用分层抽样（而非随机抽样）来创建数据的子集。在分层抽样中，数据被划分为 K 个不重叠的组，每个组的分布与整个数据集的分布相似。每个子集都会包含每个类标签的相同数量的样本，如下图所示。
图示：5 折分层交叉验证
分层抽样的优点在于确保每一折的数据中都能代表各类标签的分布，避免了类别不平衡问题，尤其是在处理类别不均衡的数据集时。通过这种方式，模型的训练和验证可以更好地反映数据的整体分布，从而提升模型的稳定性和性能。
主成分分析 (PCA)
主成分分析（PCA）是一种线性降维技术，它将一组相关的特征转换为较少的（k<p）不相关的特征，这些不相关的特征被称为主成分。通过应用PCA，我们会丢失一定量的信息，但它提供了许多好处，比如提高模型性能、减少硬件需求，并为数据可视化提供更好的理解机会。
PCA 降维的可视化示例
PCA 的核心思想是通过将数据投影到新的坐标系中，选择数据方差最大的方向作为主成分，从而在减少维度的同时保留尽可能多的数据信息。可视化时，PCA 可以帮助我们将高维数据映射到二维或三维空间，从而更容易理解和分析。
人工神经网络（ANN）
人工神经网络（ANN）灵感来源于人类大脑的结构，由多层互联的神经元组成。它们由输入层、隐藏层和输出层构成，每个神经元对传入的数据应用权重和激活函数。由于能够从数据中学习复杂的模式，人工神经网络广泛应用于图像识别、自然语言处理和预测分析等任务。
多层人工神经网络的示例
卷积神经网络（CNN）
卷积神经网络（CNN）是一种专门为图像和视频处理设计的神经网络类型。与传统的神经网络不同，后者将每个像素作为独立输入，CNN使用卷积层扫描图像，检测边缘、纹理和形状等模式。这使得CNN在识别图像中的物体时非常有效，即使物体在不同位置出现。CNN通过自动学习在视觉数据中识别模式，推动了面部识别、自动驾驶汽车和医学图像分析等技术的发展。
典型的CNN模型架构
Q学习(Q-Learning)
Q学习是一种强化学习算法，通过试验和错误的方式帮助机器学习。它通常用于游戏AI、机器人技术和自学习交易机器人。其原理很简单：“代理”（如机器人或游戏角色）与环境互动，尝试不同的动作，并根据其选择获得奖励或惩罚。随着时间的推移，代理通过将所学的内容存储在一个称为Q表的表格中，学习在不同情况下采取最佳行动。这种技术广泛应用于需要自主做出决策的AI系统，例如自动驾驶汽车在交通中导航，或者AI驱动的游戏角色学习如何下棋。
Q学习算法示例
词频-逆文档频率 (TF-IDF)
TF-IDF 是一种文本分析算法，旨在帮助识别文档中的重要词汇。它通过计算一个词出现的频率（词频，TF）以及该词在所有文档中出现的稀有程度（逆文档频率，IDF）来工作。这样可以避免像“the”和“is”这样的常见词被赋予过高的权重，同时突显出更有意义的词汇。TF-IDF 广泛应用于搜索引擎（如 Google、Bing）、关键词提取和文档排名，帮助系统理解哪些词汇与特定主题最相关。
LDA(Latent Dirichlet Allocation)
LDA(Latent Dirichlet Allocation)是一种主题建模算法，用于在大量文本集合中发现隐藏的主题。它假设每篇文档由不同的主题组成，而每个主题由一些经常一起出现的单词构成。LDA 特别适用于新闻分类、学术论文分类和客户评论分析，因为它有助于揭示大量非结构化文本中的潜在主题。如果你曾在研究工具中看到过自动主题建议功能，那么很可能它正在使用 LDA 来将相似的文本分组在一起。
图片
Word2Vec
Word2Vec 是一种自然语言处理（NLP）算法，通过将词语转换为数值向量，帮助计算机理解词语的含义。与像 TF-IDF 这样的旧方法只关注词频不同，Word2Vec 捕捉了词语之间的语义关系。例如，它可以学会“king”和“queen”之间的关系，或者“Paris”与“France”之间的关系就像“Berlin”与“Germany”之间的关系一样。这使得它在聊天机器人、情感分析和推荐系统中非常有用，因为理解词语的含义和上下文至关重要。许多现代语言模型，包括用于 Google 翻译和语音助手的模型，都依赖 Word2Vec 作为更深层次语言理解的基础。
图片
以上是常用的简明而全面地梳理关键的机器学习模型，帮助你系统掌握核心概念与应用。
