在深度学习和机器学习领域，损失函数是模型优化的核心工具之一。它不仅决定了模型的训练方向，还直接影响模型的性能和泛化能力。随着大语言模型（LLM）的兴起，对损失函数的理解和应用变得更加重要。本文将深入探讨两种常用的损失函数——KL散度和交叉熵损失，并分析它们在实际应用中的区别和联系。
1、KL散度
KL散度（Kullback-Leibler Divergence）用于衡量两个概率分布之间的相似性，常用于知识蒸馏（Knowledge Distillation）和对抗训练（Adversarial Training）等任务。其公式为：
应用场景
- 知识蒸馏：在知识蒸馏中，KL散度损失用于衡量学生模型的输出分布与教师模型的输出分布之间的差异。通过最小化这种差异，学生模型可以学习到教师模型的“知识”，从而提高性能。
- 对抗训练：KL散度损失可以用于衡量模型在对抗样本上的输出分布与真实分布之间的差异，从而增强模型的鲁棒性。
物理意义
KL散度（Kullback-Leibler Divergence）的物理意义可以从信息论和统计学的角度来理解，它是一种衡量两个概率分布之间差异的工具，具有重要的理论和实际应用价值。
- 信息论角度KL散度最初来源于信息论，用于衡量两个概率分布之间的“信息差距”。具体来说，它量化了当我们用一个概率分布Q来近似另一个概率分布P时，所导致的额外信息损失。这种信息损失可以理解为编码数据时所需的“额外比特数”，即使用Q来编码P数据时的效率损失。从熵的角度来看，KL散度可以表示为真实分布P的熵与P和Q之间的交叉熵的差值。因此，KL散度实际上衡量了使用Q而非P所引入的额外不确定性。
- 非对称性和非负性KL散度具有两个关键性质：非负性：KL散度始终大于等于零，表示两个分布之间的差异不会产生“负的信息损失”。非对称性：KL散度是不对称的，即
。这意味着选择不同的分布作为真实分布和近似分布会导致不同的结果。
KL散度定义为使用Q来编码P时的额外信息量怎么解读
- 信息量与编码在信息论中，信息量通常与编码长度相关。对于一个概率分布P，如果某个事件x发生的概率为P(x)，那么该事件的信息量可以表示为−logP(x)。这意味着概率越小的事件，其信息量越大，因为它们更“出人意料”。
- 使用Q编码P当我们使用另一个概率分布Q来编码P时，事件x的编码长度将基于Q(x)而不是P(x)。因此，事件x的编码长度变为−logQ(x)。
- 额外信息量使用Q来编码P时的额外信息量，就是基于Q的编码长度与基于P的编码长度之间的差值。对于所有可能的事件x，这个差值的期望值就是KL散度：
这个公式可以解释为：对于每个事件x，我们计算使用Q编码x时比使用P编码x多出的信息量
，然后根据P的概率分布对所有事件求和。
4. 直观理解
- 如果P(x)和Q(x)非常接近，那么
接近零，表示使用Q编码P时的额外信息量很小。 - 如果P(x)和Q(x)差距很大，那么
的绝对值很大，表示使用Q编码P时的额外信息量很大。
2、交叉熵损失
交叉熵损失函数（Cross-Entropy Loss Function）主要用于衡量模型预测的概率分布与真实标签之间的差异。
其中，p表示真实标签，q表示模型预测的标签，N表示样本数量。该公式可以看作是一个基于概率分布的比较方式，即将真实标签看做一个概率分布，将模型预测的标签也看做一个概率分布，然后计算它们之间的交叉熵。
应用场景
- 分类问题：在分类问题中，它通常用于衡量模型的预测分布与实际标签分布之间的差异。
- 下一个单词预测：在语言模型中通过最小化模型预测的概率分布与真实单词的概率分布之间的差异，用于下一个单词预测任务。
物理意义
交叉熵损失函数本质上是衡量两个概率分布之间的差异，这种差异反映了信息的“不确定性”或“信息量”。
- 信息量与不确定性在信息论中，熵（Entropy）是衡量信息不确定性的一个重要概念。熵越高，表示信息的不确定性越大；熵越低，表示信息的不确定性越小。例如，一个均匀分布的随机变量（如抛硬币）具有较高的熵，因为它包含更多的不确定性；而一个确定性事件（如抛一枚两面都是正面的硬币）的熵为零，因为它没有任何不确定性。交叉熵损失函数的核心是交叉熵（Cross-Entropy），它衡量的是模型预测的概率分布与真实分布之间的信息量。具体来说，交叉熵损失反映了模型预测分布对真实分布的“惊讶程度”或“不确定性”。
- 如果模型的预测分布与真实分布完全一致，交叉熵损失会达到最小值。
- 如果模型的预测分布与真实分布相差很大，交叉熵损失会很大，表示模型对真实结果感到“非常惊讶”。
- 信息编码与传输从信息编码的角度来看，交叉熵损失也可以理解为一种“编码代价”。假设我们用模型预测的概率分布来编码真实数据，交叉熵损失表示了这种编码所需的“平均比特数”。真实分布P表示数据的真实生成过程，模型预测的分布Q表示模型对数据生成过程的估计。如果Q与P非常接近，那么用Q来编码P所需的信息量就会很少（即交叉熵损失很小）。反之，如果Q与P差距很大，编码所需的比特数就会很多（即交叉熵损失很大）。
- 数学上的直观理解假设我们有一个二分类问题，真实标签为y∈{0,1}，模型预测为正类的概率为p。交叉熵损失可以表示为：
从这个公式可以看出，交叉熵损失惩罚了模型对真实结果的“不确定性”（即p远离真实标签）。当模型预测越准确时，损失越小，这与信息论中“减少不确定性”的目标一致。
如果真实标签y=1，损失为−log(p)。此时，p越接近 1（即预测越准确），损失越小。
如果真实标签y=0，损失为−log(1−p)。此时，p越接近 0（即预测越准确），损失越小。
分类问题为什么用交叉熵损失函数不用均方误差（MSE）
交叉熵损失函数通常在分类问题中使用，而均方误差（MSE）损失函数通常用于回归问题。这是因为分类问题和回归问题具有不同的特点和需求。
分类问题的目标是将输入样本分到不同的类别中，输出为类别的概率分布。交叉熵损失函数可以度量两个概率分布之间的差异，使得模型更好地拟合真实的类别分布。它对概率的细微差异更敏感，可以更好地区分不同的类别。此外，交叉熵损失函数在梯度计算时具有较好的数学性质，有助于更稳定地进行模型优化。
相比之下，均方误差（MSE）损失函数更适用于回归问题，其中目标是预测连续数值而不是类别。MSE损失函数度量预测值与真实值之间的差异的平方，适用于连续数值的回归问题。在分类问题中使用MSE损失函数可能不太合适，因为它对概率的微小差异不够敏感，而且在分类问题中通常需要使用激活函数（如sigmoid或softmax）将输出映射到概率空间，使得MSE的数学性质不再适用。
综上所述，交叉熵损失函数更适合分类问题，而MSE损失函数更适合回归问题。
CrossEntropyLoss基于pytorch的源代码实现
- CrossEntropyLoss的实现原理CrossEntropyLoss的计算过程可以分为两步：log_softmax：对模型的输出应用log_softmax，将输出转换为对数概率分布。
NLLLoss：计算负对数似然损失，即对真实标签对应的对数概率取负值。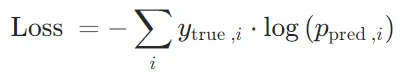
数学公式可以表示为：
其中，
是真实标签（通常是 one-hot 编码），
是模型预测的类别概率。 - PyTorch 源代码中的实现
# PyTorch 的 CrossEntropyLoss 实现
class CrossEntropyLoss(torch.nn.Module):
def __init__(self, weight=None, size_average=None, ignore_index=-100, reductinotallow='mean'):
super(CrossEntropyLoss, self).__init__()
self.weight = weight
self.ignore_index = ignore_index
self.reduction = reduction
def forward(self, input, target):
return F.cross_entropy(input, target, weight=self.weight, ignore_index=self.ignore_index, reductinotallow=self.reduction)在torch.nn.functional.cross_entropy中，实际调用了log_softmax和nll_loss：
复制def cross_entropy(input, target, weight=None, size_average=None, ignore_index=-100, reductinotallow='mean'):
return F.nll_loss(F.log_softmax(input, 1), target, weight=weight, size_average=size_average, ignore_index=ignore_index, reductinotallow=reduction)3、KL散度与交叉熵的区别
定义上的区别
- KL散度：KL散度是衡量两个概率分布P和Q之间的差异的度量。它定义为使用Q来编码P时的额外信息量，即P和Q的交叉熵与P的熵之差。
- 交叉熵：交叉熵是衡量使用一个概率分布Q来编码另一个概率分布P时所需的平均信息量。
应用上的区别
- KL散度：KL散度在深度学习中常用于衡量两个概率分布之间的差异，如在变分推断、生成模型（如VAE）、强化学习等领域。它也用于检测数据分布的漂移。
- 交叉熵：交叉熵在深度学习中主要用作损失函数，特别是在分类任务中。它用于衡量模型预测的概率分布与真实标签的概率分布之间的差异，从而指导模型的优化。
KL散度与交叉熵的关系
交叉熵可以表示为KL散度与真实分布的熵之和：
其中H(P)是真实分布P的熵。因此，最小化交叉熵等价于最小化KL散度，因为真实分布的熵是固定的。
4、其他
多任务学习各loss差异过大怎样处理
多任务学习中，如果各任务的损失差异过大，可以通过动态调整损失权重、使用任务特定的损失函数、改变模型架构或引入正则化等方法来处理。目标是平衡各任务的贡献，以便更好地训练模型。
如果softmax的e次方超过float的值了怎么办
- 可以使用数值稳定性技巧来避免溢出。具体来说，可以在计算
之前从每个
中减去 x 中的最大值
：
- 使用对数概率来避免溢出对数函数log(x)具有将乘法运算转换为加法运算的性质：
这使得在处理非常小或非常大的概率值时，可以避免直接相乘导致的数值下溢（underflow）或上溢（overflow）。在计算交叉熵损失时，可以使用log_softmax，公式为：
